Rotation Transformation#

A rotation transformation modifies the orientation of an object by applying time-dependent or static rotations to its local frame.

Rotation Modes#

Transform Type

Mode

Description

Rotation

Constant

The object retains its original orientation throughout the simulation.

Euler_Angle

Applies a time-dependent rotation using Euler angles. See Euler Angle section below.

—

Mathematical Model#

If a rotation transformation is applied, the position vector \(\mathbf{P}_{B}`\) (resulting from flexibility trans) is further transformed by the rotation matrix \(\mathbf{R}_{B}\):

\[\mathbf{P}_{B}'' = \mathbf{R}_{B} \cdot \mathbf{P}_{B}'\]

The rotation matrix is computed from Euler angles if the Euler_Angle mode is selected. The rotation matrix is defined as:

\[\mathbf{R}_{B} = \mathbf{R}_{\text{axis}_1}(\theta_{1}) \cdot \mathbf{R}_{\text{axis}_2}(\theta_{2}) \cdot \mathbf{R}_{\text{axis}_3}(\theta_{3})\]

Here, \(\mathbf{R}_{\text{axis}_i}(\theta)\) denotes the rotation matrix for a rotation of angle \(\theta\) about the body-fixed axis \(\text{axis}_i\), constructed so that it operates exclusively on that axis—i.e., it ignores any rotations about the other axes \(\text{axis}_j\) for \(j \neq i\).

Example: For rotation sequence (X, Y, Z):

\[\mathbf{R}_{B} = \mathbf{R}_{X}(\theta_{1}) \cdot \mathbf{R}_{Y}(\theta_{2}) \cdot \mathbf{R}_{Z}(\theta_{3})\]

—

Else if the Constant mode is selected, the rotation matrix is set to the identity matrix:

\[\begin{split}\mathbf{R}_{B} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{split}\]

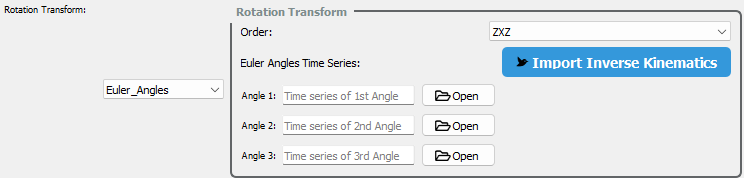
Euler Angle#

The Euler_Angle mode applies time-dependent rotations using Euler angles. This mode allows for detailed control of an object’s orientation over time by specifying a rotation sequence and supplying angle data for each frame.

Overview#

Rotation is applied through a user-defined sequence of three intrinsic (body-fixed) rotations—commonly ZYX, XYZ, etc. In body frame terms X - \(\hat{\mathbf{b}}_1\), Y - \(\hat{\mathbf{b}}_2\), and Z - \(\hat{\mathbf{b}}_3\). The rotation sequence is defined as:

  • \(\theta_{1}\): Rotation about \(\mathbf{axis}_1\).

  • \(\theta_{2}\): Rotation about \(\mathbf{axis}_2\).

  • \(\theta_{3}\): Rotation about \(\mathbf{axis}_3\).

The rotation matrix is computed as:

\[\mathbf{R}_{B} = \mathbf{R}_{\text{axis}_1}(\theta_{1}) \cdot \mathbf{R}_{\text{axis}_2}(\theta_{2}) \cdot \mathbf{R}_{\text{axis}_3}(\theta_{3})\]

Example: For rotation sequence (Z, Y, X):

\[\mathbf{R}_{B} = \mathbf{R}_{Z}(\theta_{1}) \cdot \mathbf{R}_{Y}(\theta_{2}) \cdot \mathbf{R}_{X}(\theta_{3})\]

Input Options#

Users may provide Euler angle sequences in two ways:

  • CSV File Input: Upload a file with time-varying angle values.

  • Automatic Import: Import angle sequences directly from the Inverse kinematics module.

This flexibility supports both manual design and automated workflows.

Euler Angle Rotation Transform

Note

Euler Angle CSV Format

When using Euler rotations, you must provide three separate CSV files—one for each rotation angle:

  • Angle I: Rotation about the first axis in your chosen Euler sequence.

  • Angle II: Rotation about the second axis.

  • Angle III: Rotation about the third axis.

For example, in a (Z, Y, X) rotation sequence: - Angle I refers to rotation around the Z-axis, - Angle II around the Y-axis, and - Angle III around the X-axis.

CSV Format Requirements:

  • Each file must contain a single column of angle values (in degrees).

  • Each row represents the angle at a given time step.

  • No header row should be included.

Example (`angle_1.csv`):

0.0
12.5
25.0
18.2
...

Similarly, create angle_2.csv and angle_3.csv to represent the remaining two angles in the sequence.

Usage Notes#

  • Euler angles must be in radians

  • Ensure time series length matches the number of animation frames

—